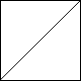
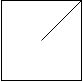
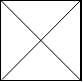
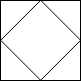
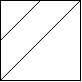
由斜杠划分的区域

一月份 Leetcode 的每日一题几乎都是并查集. 不过个人认为与状态转移方程千变万化的动态规划相比, 并查集还是相对比较简单的. 这道题是我觉得最有趣的两道之一 (另一道是打砖块, 以后有时间的话也写一篇它的题解).

题目源自 Leetcode 959 题

在由 1 x 1 方格组成的 N x N 网格 grid 中，每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。

（请注意，反斜杠字符是转义的，因此 \ 用 “\\” 表示。）

返回区域的数目。

示例 1：

输入：
[
  ” /“,
 ”/ “
]
输出：2
解释：2x2 网格如下：

示例 2：

输入：
[
  ” /“,
 ” “
]
输出：1
解释：2x2 网格如下：

示例 3：

输入：
[
  “\\/”,
  “/\\”
]
输出：4
解释：（回想一下，因为 \ 字符是转义的，所以 “\\/” 表示 \/，而 “/\\” 表示 /\。）
2x2 网格如下：

示例 4：

输入：
[
  “/\\”,
  “\\/”
]
输出：5
解释：（回想一下，因为 \ 字符是转义的，所以 “/\\” 表示 /\，而 “\\/” 表示 \/。）
2x2 网格如下：

示例 5：

输入：
[
  “//”,
  “/”
]
输出：3
解释：2x2 网格如下：

提示：

1. 1 <= grid.length == grid[0].length <= 30
2. grid[i][j] 是 ‘/’、‘\’、或 ’ ’。

容易想到, 这是一个求图的连通分量的个数问题. 因此思路分两步:

1. 将斜杠 / 反斜杠 \ 和空格表示的网格抽象成图;
2. 求图的连通分量的个数.

abstract

如上图所示, 如果我们将上图左边的网格转换成右边的图, 我们就能很快地使用一些图算法求出图的连通分量的数量, 这也就是网格中区域的数量.

并查集

并查集, 算法导论 中称为不相交集合的数据结构(Disjoint-set data structure), 在第 21 章中有介绍. 也可以看这篇文章, 讲解地很清楚. 这里我 (因为懒) 就不做过多的介绍. 简单地来说就是遍历图的每条边, 依次合并每条边连接的两个节点; 最终若节点 i 与 节点 j 连通, 必然有 find(i) == find(j).

这里我们使用的路径压缩的并查集算法. 我们使用数组 pi (\(\pi\), 谐音 parent) 存储每个节点的父节点.

pi = list(range(n)) # 初始化 n 个节点的并查集, pi[i] = i

def find(k):
    if pi[k] != k:
        pi[k] = find(pi[k]) # 路径压缩
    return pi[k]

def merge(i, j):
    pi[find(i)] = find(j)

将网格抽象成图

每个格子要么是 /, 要么是 \, 要么是空格. 我们可以认为每个格子都是由两个节点组成, 因此可以给每个格子分配两个节点编号. 对于空格来说, 这两个节点是相连的; 对于 / 和 \, 它们的节点分布如下图所示:

abstract

我们规定, 若靠左的节点 (即上图中的 0 号节点) 编号为 \(k\), 则靠右的节点 (上图中的 1 号节点) 编号为 \(k + 1\). 对于一个 \(N\times N\) 的网格中 \(i\) 行 \(j\) 列的格子的两个节点编号分别是 \(2(iN + j)\) 和 \(2(iN + j) + 1\).

使用并查集, 我们需要依次遍历一个图的所有边, 依次 merge 每条边连通的两个节点. 我们可以遍历网格中的每个格子, 然后考虑这个格子的节点和与其相邻的格子的节点之间的连通性, 依次 merge 即可. 因为是无向图, 节点 a 连通 b 也意味着 b 连通 a, 因此每个格子都只需要考虑上方和左边的格子. 对于左边的格子, 如下图所示, 无论如何都是 0 号节点与左边格子的 1 号节点相连:

abstract

对于上方的格子, 就有四种情况. 我们可根据当前格子和上方格子是 / 还是 \ 判断应该 merge 哪两个节点.

abstract

当然, 如果当前格子是空格, 还要 merge 它的两个节点.

最终代码如下:

def regionsBySlashes(grid):
    N = len(grid)
    pi = list(range(N * N * 2)) # 初始化 N * N * 2 个节点的并查集
    def find(k):
        if pi[k] != k:
            pi[k] = find(pi[k])
        return pi[k]
    def merge(i, j):
        pi[find(i)] = find(j)

    for i in range(N):
        for j in range(N):
            c = grid[i][j]
            k = 2*(i*N + j)
            if c == ' ': # 空格, merge 它的两个节点
                merge(k, k + 1)

            if i > 0: # merge 上方格子的节点
                C = grid[i-1][j]
                K = 2*((i-1)*N + j)
                m = k if c == '/' else k + 1
                n = K if C == '\\' else K + 1
                merge(m, n)

            if j > 0: # merge 左边格子的节点
                K = 2*(i*N + j-1)
                merge(k, K + 1)

    ans = 0
    for i in range(N * N * 2):
        if find(i) == i:
            ans += 1

    return ans