牛顿迭代法求平方根
1.先说结论
迭代若干次, 当
1 | |
2.详解
牛顿迭代法是一种近似求多项式方程根的一种方法.
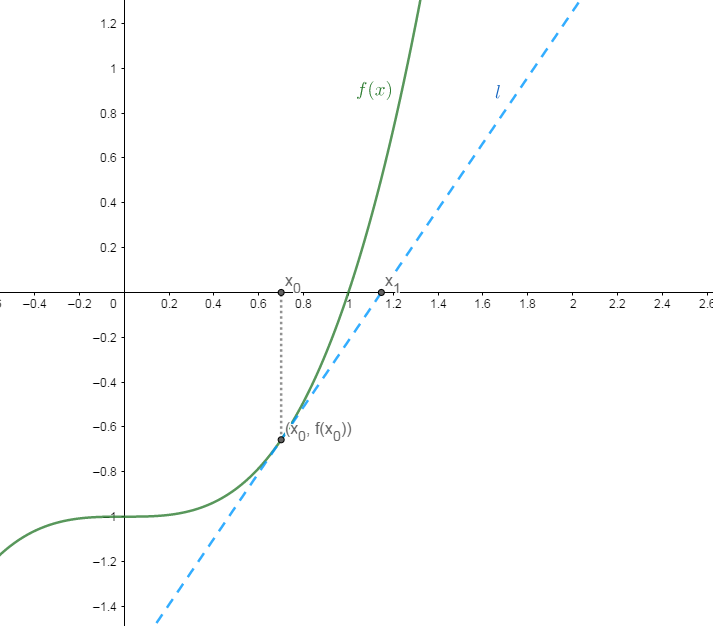
如图所示, 对于方程
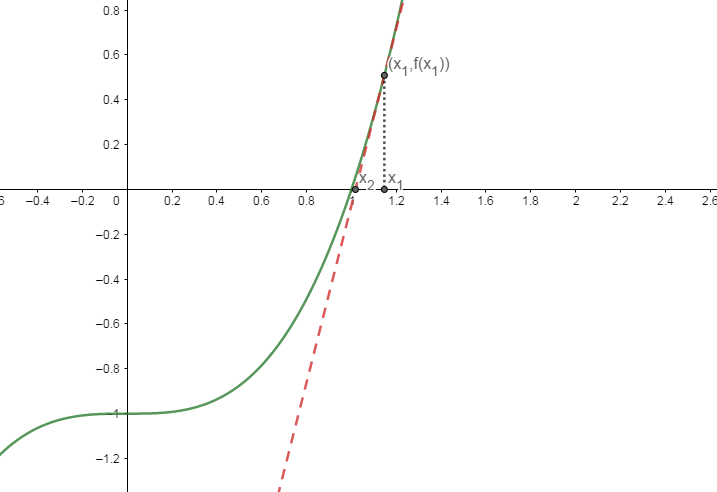
重复以上操作, 分别计算出
最终
(2) 式被称为牛顿迭代公式
用牛顿迭代法求
也就得到了文章开头所列出的 (1) 式.
牛顿迭代法求平方根
https://luyuhuang.tech/2019/09/17/sqrt.html
迭代若干次, 当
1 | |
牛顿迭代法是一种近似求多项式方程根的一种方法.

如图所示, 对于方程
重复以上操作, 分别计算出

最终
(2) 式被称为牛顿迭代公式
用牛顿迭代法求
也就得到了文章开头所列出的 (1) 式.