解数独算法

1. 引言

数独是一种经典的数字游戏, 玩家需要在一个 9*9 的棋盘上填数字, 保证每一行, 每一列和每一个小九宫格里的数字都是 1-9 且没有重复. 通常盘面上会给出一些提示数让玩家推导.

sudoku

通常数独的解是唯一的, 但随着提示数的减少, 数独也可以有多个解; 极端情况下, 没有提示数, 数独也是可以解的, 只不过解的数量会非常多. 本文讨论解数独的算法, 并且尝试求出一个数独的所有可行解.

2. 合法的数

我们来看数独的规则:

玩家需要在一个 9*9 的棋盘上填数字, 保证每一行, 每一列和每一个小九宫格里的数字都是 1-9 且没有重复.

首先我们需要根据任意一个给定的棋盘, 快速地得出任意一个空白格子上可填的数. 怎样做到这一点呢? 遍历这个格子所在的行, 列和小九宫格吗? 那太慢了. 正确的做法是使用集合. 对于每一行, 每一列和每一个小九宫格, 我们都维护一个集合, 记录这一行, 这一列或这一个小九宫格上填过的数字. 这样一来, 对于任意一个空白格子, 我们都能快速得出那些数字可以填.

因为数独只能填数字 1-9, 因此一种比较好的集合表示法是使用位图(bitmap), 这样一个整数就能表示一个集合: 数字 i 在集合中, 当且仅当这个整数第 i 二进制位为 1. 插入和删除也比较简单, 分别按位或和按位与即可:

1
2
3
4
5
6
7
8
9
void add_to_set(int &set, int n) {
    set |= 1 << n
}
void remove_from_set(int &set, int n) {
    set &= ~(1 << n);
}
bool is_in_set(int set, int n) {
    return set & n;
}

我们给每一行, 每一列和每一个小九宫格编号, 如图所示:

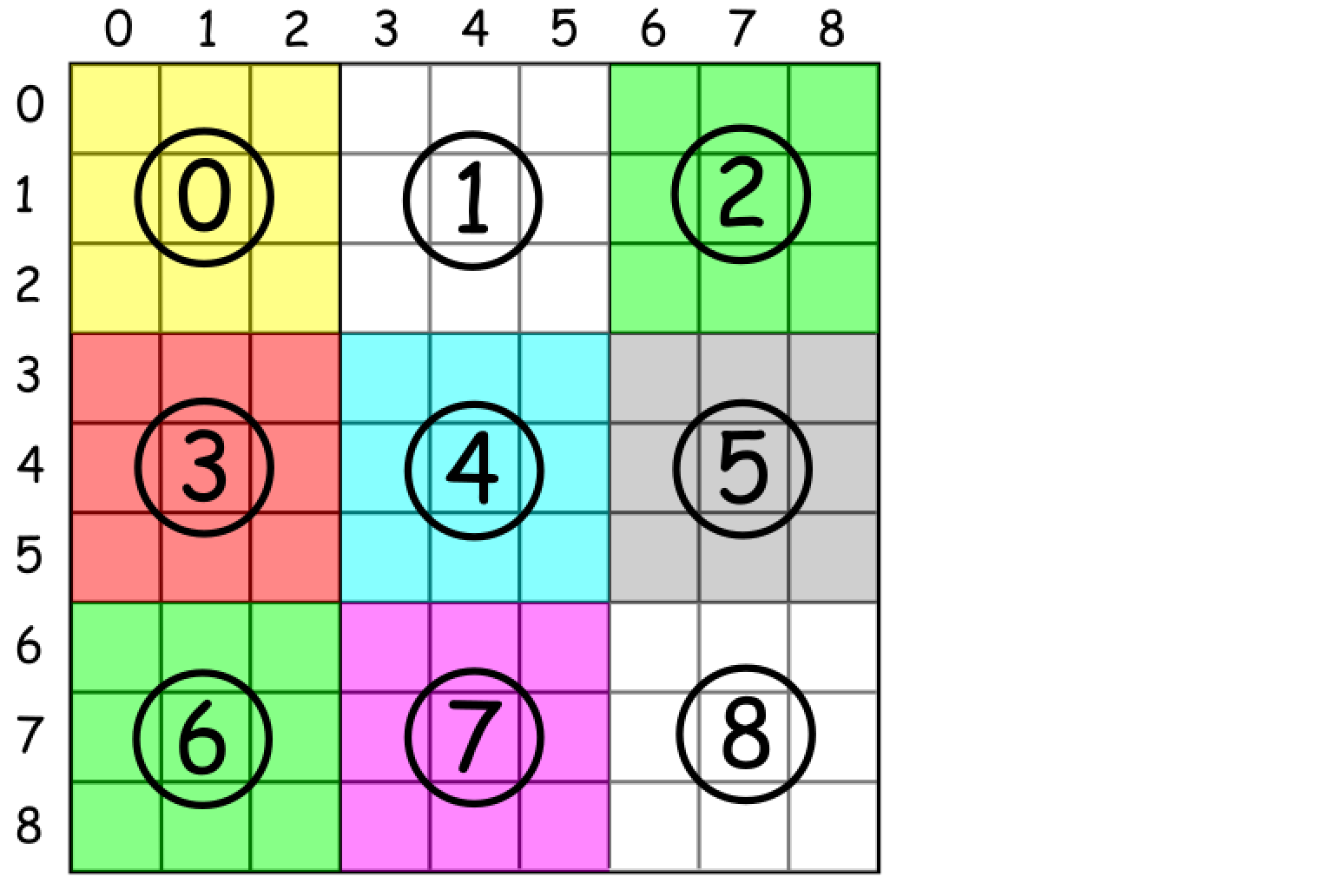
sudoku

那么对于一个第 i 行, 第 j 列的格子, 它处于哪个小九宫格呢? 很简单, 作下除法就好了:

1
2
3
int get_box(int i, int j) {
    return i / 3 * 3 + j / 3;
}

这样我们就可以把这些集合存起来了. 我们一共需要存储 27 个集合(其实就是 27 个整数)

1
2
3
int m_rows[9];
int m_cols[9];
int m_boxes[9];

这样, 对于任意一个第 i 行, 第 j 列的格子, 我们很快能够判断哪些数能填, 哪些数不能填:

1
2
3
4
bool can_set(int i, int j, int n) {
    int bit = 1 << n;
    return !(m_rows[i] & bit) && !(m_cols[j] & bit) && !(m_boxes[get_box(i, j)] & bit);
}

3. 回溯法

回溯法是解数独算法的核心.

判断了一个空白格子的合法数之后, 我们该如何得到一个可行解呢? 一共有数十个格子(最多 81 个格子)等着我们去填呢, 难道写 81 重循环一个个去试吗? 当然不行. 正确的做法是使用回溯法.

所谓的回溯法, 通俗地讲就是: 你可以想象我们的算法在走迷宫, 摆在我们面前有很多条路可走, 不知道该走哪一条; 不过没关系, 我们随便走一条, 并且记录下我们在哪个岔道口走了哪条路; 万一走着走着无路可走了, 我们再回来, 再选另一条路走, 直到找到正确的路为止. 听着是不是有点像深度优先遍历? 没错, 深度优先遍历就是一种典型的回溯法.

例如, 在下图中, 根据 §2 所讨论的, 我们可以快速得出粉色格子中可填的数为 1, 2, 4. 到底该填哪一个数呢? 不知道. 不过没关系, 我们先填 1 试试:

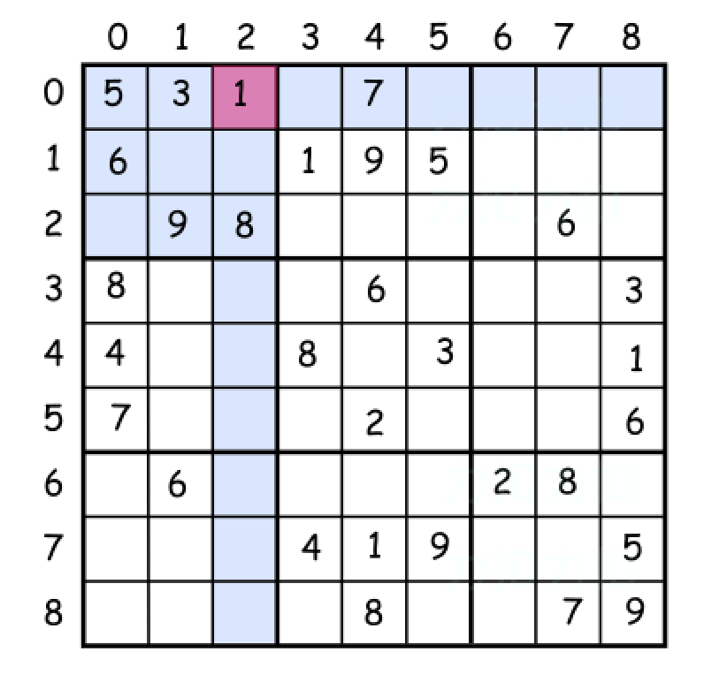
sudoku

然后以此类推, 发现填到第 9 个格子就填不下去了! 这意味着我们走到 “死胡同” 里了. 怎么办? 这个时候我们就回溯: 一个格子一个格子地回退, 重新作选择, 直到解出数独为止. 这便是回溯法.

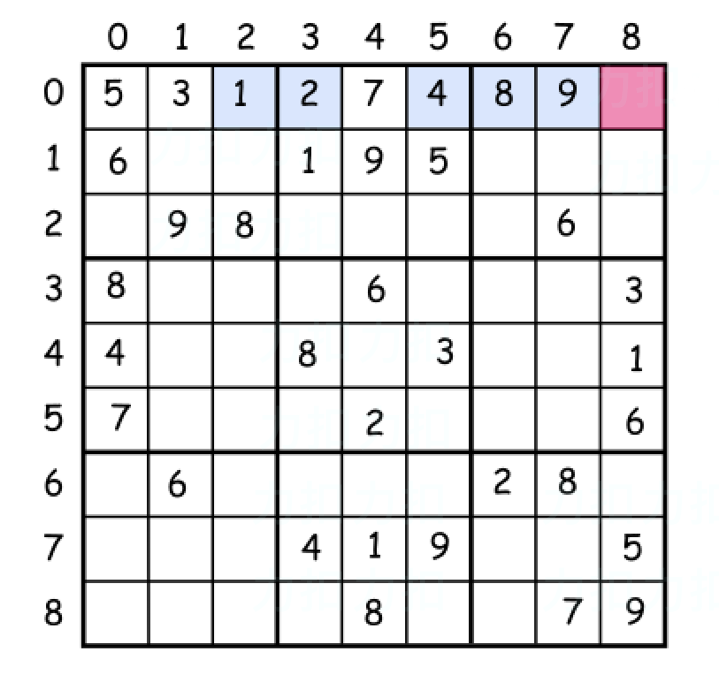
sudoku

与深度优先遍历类似, 我们可以利用递归算法, 每次递归调用便是迭代, 每次递归调用返回便是回溯. 这样每次作的选择都保存在调用栈里. 代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
void set_num(int i, int j, int n) {
    int bit = 1 << n;
    /*add to set*/
    m_rows[i] |= bit;
    m_cols[j] |= bit;
    m_boxes[get_box(i, j)] |= bit;

    m_lattice[i][j] = n;
}

void del_num(int i, int j, int n) {
    int bit = ~(1 << n);
    /*remove from set*/
    m_rows[i] &= bit;
    m_cols[j] &= bit;
    m_boxes[get_box(i, j)] &= bit;

    m_lattice[i][j] = 0;
}

void backtrack(int i, int j) {
    if (i >= 9) {
        m_done = true; //sudoku solved
        return;
    }

    if (m_lattice[i][j] == 0) {
        for (int t = 1; t <= 9; ++t) { // try all number in 1-9
            if (can_set(i, j, t)) {
                set_num(i, j, t);
                backtrack(i + (j + 1) / 9, (j + 1) % 9); // try next lattice
                if (m_done) break;
                /* if backtrack returned and m_done is false, it's means we
                 * went a wrong rode, we should delete it and try next number */
                del_num(i, j, t);
            }
        }
    } else {
        /*if it isn't a empty lattice, try next lattice directly*/
        backtrack(i + (j + 1) / 9, (j + 1) % 9);
    }
}

代码讲解见注释. 现在只需调用 backtrack(0, 0) 待其返回, m_lattice 就被填满了数独的解.

4. 改递归为迭代

§3 给出的算法可以得到数独的一个可行解, 但是得不到数独的全部可行解. 也可以在它的基础上稍作修改, 当 i >= 9 的时候把解存其来然后让它接着跑, 不过我不想这样. 我希望提供一个方法, 每调用一次, 就计算出一个可行解; 如果没有可行解了, 就返回一个值告诉调用者. 就像游标一样. 为了做到这一点, 我们就不能用调用栈保存信息了, 我们需要把递归改成迭代, 然后自己建一个栈保存信息.

前面说了, 回溯法要保存 “在哪个岔道口走了哪条路”. 观察下 §3 的算法, 我们需要保存的信息就是哪个格子选择了哪个数字. 我们用一个三元组 (i, j, n) 表示 i 行 j 列的格子选择了数字 n. 因此栈就是这样的:

1
std::vector<std::tuple<int, int, int> > m_stack;

三元组 (i, j, n) 中的 n 至关重要. 想象一个格子填了 1, 然后在后续的迭代中走入了 “死胡同”, 回溯回来了, 这时候应该把这个格子上的数字 1 删掉, 然后重新从 2 开始选择数字. 因此每次填数字时都应该更新 n, 每次选择数字时都应该从 n + 1 开始选择, n 初始应该为 0. 此外我们还可以通过判断 n 是否为 0 来判断这个格子是迭代而来, 还是回溯而来.

因为我们从左上角开始依次迭代, 因此我们初始把 (0, 0, 0) 入栈.

1
m_stack.emplace_back(0, 0, 0);

迭代的整体流程是不断地取栈顶元素, 对每个格子尝试 1-9 的全部数字. 每次找到一个可行的数字, 就填入可行数字, 把下一个格子入栈; 尝试完毕或者无解, 就退栈, 进行回溯. 直到栈为空.

退栈的时候需要把提示数的格子也退了, 因为一旦遇到提示数, 就会立刻迭代下一个格子, 导致死循环.

与递归算法不同, 我们不能通过判断 m_lattice[i][j] == 0 来区分一个格子是否是提示数格子, 因为每填一个数都会把数字置入 m_lattice 中(递归法能这样做是因为递归法在填数之前就已经判断好了). 因此我们把原始的格子存在变量 m_origin 中, 通过判断 m_origin[i * 9 + j] == 0 来区分是否是提示数格子.(m_origin是 int* 类型, 用指针表示二维数组.)

迭代算法和递归算法比较类似, 不同的是需要我们自己维护栈. 代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void back_stack() {
    do {
        m_stack.pop_back();
    } while (!m_stack.empty() && std::get<2>(*(m_stack.end() - 1)) == 0);
}

bool calc() {
    while (!m_stack.empty()) {
        auto pair = m_stack.end() - 1;
        int i = std::get<0>(*pair), j = std::get<1>(*pair);
        int n = std::get<2>(*pair);

        if (i >= 9) {
            back_stack(); // find a solution, back stack for next call
            return true;
        }

        /* from backtrace, delete it and try next number*/
        if (n > 0) del_num(i, j, n);

        if (m_origin[i * 9 + j] == 0) {
            bool setted = false;
            for (int t = n + 1; t <= 9; ++t) {
                if (can_set(i, j, t)) {
                    set_num(i, j, t);
                    std::get<2>(*pair) = t;
                    m_stack.emplace_back(i + (j + 1) / 9, (j + 1) % 9, 0);
                    setted = true;
                    break;
                }
            }
            if (!setted)
                back_stack();

        } else {
            m_stack.emplace_back(i + (j + 1) / 9, (j + 1) % 9, 0);
        }
    }

    return false;
}

现在每次调用 calc(), 若其返回 true 说明得到一个可行解, 可以在 m_lattice 拿到它; 否则没有可行解.

5. 总结

完整代码见 Sudoku-Solution

关于 Sudoku-Solution

这个项目之前是笔者上大学时刚学会 C++, 对着网上的教程强撸出来的. 虽然撸出来了, 却不谙其中思想, 如今回过头来看惨不忍睹. 现在笔者重新捋清思路, 把代码完全重写了, 并且写了这篇文章.

本文主要讨论了解数独算法的思想及实现, 和回溯法的一般思路. 希望对大家有所帮助.

参考资料: 解数独

#algorithms #featured
解数独算法
https://luyuhuang.tech/2019/10/07/sudoku-solution.html
Author
Luyu Huang
Posted on
October 7, 2019
Licensed under